医学部東大早慶受験塾ナンバースクール予備校～医大、東京大学、早稲田・慶応・国公立・難関大コース～高卒・浪人・宅浪・仮面浪人・大学浪人生対象

医学部東大早慶受験専門塾ナンバースクール～NumberSchool予備校は、最高の講師陣による受験ノウハウと『オーダーメイドシステム』で、1人ひとりの学習目的に全力対応します。渋谷、神保町、五反田、浅草橋、北千住を拠点に表参道、青山、原宿、大崎、新大久保、神田、駒込、錦糸町、王子、川崎、東新宿、自由が丘、銀座、東日本橋、馬喰町、竹橋、築地、竹ノ塚、本八幡、取手、浦和、大宮、久喜など東京都内および神奈川県・埼玉県・千葉県・茨城県で講習しています。

医大数学、理系数学、文系数学、英語、その他全教科で充実のカリキュラム

担当クラスは国立・早慶上智大以上、うち50％以上を東大・京大合格に導くプロ専任講師による講習

東大院・東大・早慶講師による抜群の講習

一般的な予備校では物足りないハイレベルな講義や演習を学ぶことで、受験生からは、予備校にありがちな一方的な講習ではなく、少人数・個別制のメリットといえる質問のし易さと学習時間の柔軟性で好評を得ています。

個別対応・家庭教師等で、効果を上げる講習も魅力です。

他の予備校の授業手続きをしたにもかかわらずセカンドスクールとして、ナンバースクールの数学や英語を月数回、予備校終了後から夜9時までの空いている時間帯で学ぶ受験生もいます。

東京慈恵医大、東京医大、埼玉医大、獨協医大、防衛医大、自治医大など私立医学部入試についても、受験校毎の個別対応・家庭教師で医学部受験をサポートしています。

ご質問・ご相談はメールにてご連絡ください。

電話での対応をご希望の方は、
(連絡先)
までご連絡ください。

☆受験大学に応じた傾向分析による対策
☆豊富な演習時間とテーマ別題材の充実
☆年間割引、複数科目割引制度実施。無理のない講習費
☆苦手科目・項目については、応用につながる基本事項の確認など基礎から安心の個別講習実施
☆学習相談を効果的に利用し、医学部東大難関大受験を目指す人に最適なコースを提供

☆東大・東工大・京大・東大理科Ⅲ類・慶大医学部など難関医大医学部を目指す上級者にはよりハイレベル・リッチな入試用教材を提供
⇒　東工大AO入試の難問題とナンバースクールならではの解答を一部公開しました。
   (内部生には、他に類を見ない全問完全解答を、試験直後に講習しました。)

難関大学合格者が利用している重要なテキスト・学習書の提供

詳しくは、早めに無料の学習相談でお問合せください。

 

各教科について、以下の「数学コース例」を参考にしてください。
  （不明な点は、無料の学習相談としてご連絡ください。）

 

（コース例 ： 「文理共通数学」の場合↓＜第１ステージ＞～＜第６ステージ＞６段階制）

 

[一般共通コース］　＜第１ステージ＞～＜第３ステージ＞

（＜第０ステージ＞　学校の授業レベルでの教科書・問題集の一般的な理解度の段階）

 

＜第１ステージ＞　教科書の徹底補強。一般に教科書の公式は使えても、その公式を証明できない。さらに、公式の証明のアイディアがどのように受験問題に使われているか知らないなど、教科書を本格的には理解していない傾向があります。

中学３年生の教科書を例にすると、

「(x-2)(x-3)=0　⇒　x-2=0　or　x-3=0　が真であること（命題の逆は明らかに真）」、および

「三平方の定理の証明（教科書的方法・アインシュタインの方法など）とその逆の命題の真」が差のつく部分です。

「直角三角形　ならば　a²+b²=c²」（三平方の定理）　の証明は当然として、中学の教科書レベルで昔から差のつくのは、"三平方の定理の証明の逆"「a²+b²=c² ならば　直角三角形」を認識しているかで差がつきます。

その他にも、中学１年時の難問「ax=b　を解け」に対して、一般の高校生でも解けないケースが多々みられます。

⇒　答えは、「(i)a≠0のとき、x=b/a 　(ii)a=0かつb=0のとき、xは全ての数　(iii)a=0かつb≠0のとき、xは解なし」

その他、高校数学「数学Ⅰ」を例にすると、「任意の実数xについて、方程式 ax²+bx+c>0 が成り立つためのa,b,cの条件を求めよ。」についても正確に答えられないケースがみられます。実際、勝手に２次方程式と思い込み、「a=0,b=0,c>0」の条件を忘れ、「a>0,b²-4ac<0」の条件しか考えないケースがみられます。

また、高校数学「数学Ⅱ」を例にすると、三角関数の加法定理の公式は記憶に残り使えますが、その証明を何通りかの方法で示すとなるとできない場合は、応用力に欠けてきます。応用問題を苦手とする理由に、核となる基本事項の認識ができていない問題点が挙げられます。

東京大学の前期の入試問題で、この問題点をストレートに指摘した公式証明の良問がありました。

 

また、多くの受験生の弱点として、点と直線の距離公式は使えるが、その証明を簡単な原理で理解されていないなどの現状があります。この理由としては、教科書の証明の方法が機械的であり、図と式の一体性に欠けることが原因の一つといえます。

例えば、ナンバースクールでは、この公式の成り立ちを以下のように多面的な視点から考察し検討します。さらに、空間への拡張として、点と平面の距離公式も同様に考察します。

点と直線の距離公式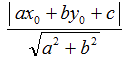

1. 直線のパラメータ表示を時間感覚で認識し、1秒間に進む方向ベクトルの長さを利用して、数式の構造を理解する方法
2. ベクトルの内積を利用した考察、さらに、単位ベクトルの内積の利用との比較
3. 点から直線までのベクトルと法線ベクトルとの平行条件を利用した解法
4. 原点から直線までの距離を求め、変換・逆変換の手法で一般化する方法
5. 三角形の相似比を利用した考察
6. 教科書的な方法との比較・検討

本ステージでは、教科書完全理解を追求し、応用問題を解く基礎固めの講習を徹底します。

この＜第１ステージ＞で、応用力育成につなげるテクニックがNumber School の最大の強みです。

＜第２ステージ＞　応用問題を解くために必要な最重要基本問題と受験参考書で扱われる内容を各単元ごとに完璧に解説・演習する講座です。

受験用参考書およびセンター試験レベルを超える内容も加わります。

すべてNumber School のオリジナル教材です。

 

＜第３ステージ＞　上記ステージにより、応用問題を解くための基礎固めができました。本ステージは、センター試験レベルを超えるハイレベルな良質問題を解く演習主体の講座です。

ただし、演習で問題意識を高めた後、次に述べる＜第４ステージ＞の数学者としての観点からハイレベルな解説を実施します。

この演習を終えた段階で、センター試験85～100点の効果があります。

 

********以下、医学部東大難関大コース（プロ講師担当）********

[医学部東大難関大コース］　＜第４ステージ＞～＜第６ステージ＞

＜第４ステージ＞　歴史的大数学者が好んで研究して得た重要な数学的アイディアが、過去から将来の受験問題に応用されて、脈々と受け継がれていきます。

受講者が思わず声を上げてしまうような感動的な数学を味わうことができる「トピック数学」とその応用演習です。

最終的には受験問題との関わりを研究します。

 

難関大での受験問題には、昔から以下の内容を題材にした良問が出題されています。

[解析編]
ロピタルの定理、ウォリスの公式
テイラー・マクローリン展開

オイラーの公式、正n角形と複素数解
チェビシェフの多項式 cos(nθ)=f(cosθ)
tan(nθ) の展開式
逆関数の積分（ヤングの不等式）

[行列編]（旧課程）
一次変換、合成変換、ベクトルの一次独立と一次従属
方程式の解
行列のn乗（10通りの解法）
数学的帰納法、漸化式、ケイリー・ハミルトンの定理、三項間漸化式、
固有値・固有ベクトル、対角化行列 P^-1AP=D
スペクトル分解(1)、スペクトル分解(2)
重解固有値
ジョルダン標準形

[応用数学編]
コーシー・シュワルツの不等式
外積と行列式
完全順列とモンモール問題
ｅが無理数であることの証明
特殊解と一般解（漸化式、整数解、微分方程式）
球面三角法
双曲関数の微積分

二項分布の極限が正規分布曲線の証明

ロジスティック曲線（成長曲線）とハイパボリックタンジェント

特殊相対性理論の影

[整数問題]
ピタゴラス数と整数論
不定方程式の解
フェルマーと無限降下法

［トピック数学］

オイラーの定理　／　 オイラーの公式　／　 オイラー関数　／　 オイラー定数　／　 ガウスの発散定理　／　 ストークスの定理　／　 パップスの定理　／　 チェバの定理　／　 メネラウスの定理　／　 ナポレオンの定理　／　 ナポレオン点　／　 第一フェルマー点　／　 フェルマーの小定理　／　 フェルマーの大定理と拡張　／　 無限降下法　／　 ハミルトン・ケーリーの公式　／　 三平方の定理（多次元）　／　 ロピタルの定理　／　 ウォリスの公式　／　 ぺル方程式　／　 ラグランジェの補間法　／　 ベジェ曲線　／　 パップス-ギュルダンの定理　／　 チェビシェフ多項式　／　 tan(nθ)　／　 格子点　／　 正ｎ角形と格子点　／　 ピックの定理　／　 モーリーの定理　／　 モンモールの問題（完全順列）　／　 スチュワートの定理　／　 鳩ノ巣原理　／　 ジョルダン標準形　／　 正多面体の体積・性質

 

＜第５ステージ＞　難関大学の年度別に総合過去問題演習を行います。＜第１ステージ＞から＜第４ステージ＞までで得た知識との関連を留意した解説がみものです。

大阪大、千葉大、東北大、北海道大学、私立医大などの年度別の演習・解説となりますが、京都大の良問を中心に学習し、次の＜第６ステージ＞への橋渡しとなります。

 

＜第６ステージ＞医学部・東大・東工大などの最難関大学の過去問題演習とその背景を重視した解説を行います。さらに、数学の本質と難問数学の原点といえるアイディアが豊富なバイブル「解析概論」をベースに、将来工学系・理系分野に進学するためのハイレベルな講習を行います。

特に、この段階では、受験大学の傾向把握に向けた個別指導も行っています。

*********************

 

［英語コース］

英語についても上記数学講習と同様な流れとなります。

最良の方法は受験校を早期に特定し、その傾向に向けた学習をすることです。

そのため、早期に個別学習相談を行い継続的に学習の方法を見直していきます。

 

東大英語を例にとりますと、問題の多様性と量の多さです。

長文読解、和訳、文法・語法、英作文、要約、リスニングなどの多岐に渡る日々の学習努力が欠かせません。

特に、文章の流れを瞬時につかむだけでなく、題材の根拠や具体性、さらに、論理的な解釈が求められます。

基礎的な文法・語彙の知識は必要不可欠なのは勿論ですが、特殊なものより極めて標準的な英語能力を身につける必要があります。
不明な点は、無料の学習相談としてご連絡ください。